Info Tekno dan Hiburan Terbaru
Info seputar gadget, tekno, games, lifestyle, dan hiburan lainnya yang menarik, kami sajikan dengan ringkas untuk anda.
Artikel Terbaru

10 Kamera Panasonic Lumix Terbaik dan Spesifikasinya
Compact Camera atau dikenal juga dengan kamera saku memang perlahan mulai tergerus popularitasnya seiring meningkatnya …

10 Kamera Fujifilm Murah Terbaik
Fujifilm adalah pemain lama dalam dunia optik dan kamera digital yang sudah memulai kiprahnya sejak …

Ini Deretan 10 Kamera Mirrorless Olympus Terbaik
Akhir-akhir ini, kamera mirrorless semakin populer di kalangan pecinta fotografi. Oleh sebab itu, berikut ini …

Review Asus Zenfone Go (ZB452KG), Harga dan Spesifikasi
Satu lagi produk HP dari Asus dengan inovasi terkini. Asus Zenfone Go (ZB452KG). Berbeda dengan …

Spesifikasi dan Harga Asus Zenfone 3 Laser (ZC551KL) Terbaru
Memenuhi kebutuhan pengguna HP, Asus kembali meluncurkan produk bernama Asus Zenfone 3 Laser (ZC551KL). Produk …
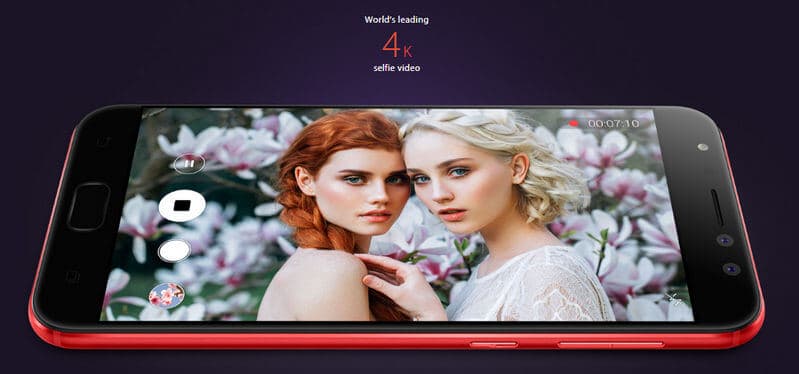
Review Harga dan Spesifikasi Asus Zenfone 4 Selfie Pro (ZD552KL)
Hanya dua bulan setelah meluncurkan Zenfone 4 Selfie (ZD553KL) pada Agustus 2017, Asus kembali menambah …

Review Harga Asus Zenfone Zoom S (ZE553KL) dan Spesifikasi
Asus benar-benar mempertahankan keunggulannya dalam memadukan teknologi dan gaya hidup. Satu lagi produk Asus yang …

Kelebihan dan Kekurangan Asus Zenfone 5Q, Harga dan Spesifikasi
Asus benar-benar mempertahankan keunggulannya dalam memadukan teknologi dan gaya hidup. Satu lagi produk Asus yang …

Harga Asus Zenfone 3 Max, Spesifikasi, Kelebihan dan Kekurangannya
Satu lagi produk Asus yang menerapkan kebutuhan akan gaya hidup pengguna HP yang diluncurkan pada …

Spesifikasi dan Harga Asus Zenfone 4 Max (ZC520KL)
Asus masih terus mempertahankan keunggulannya dalam memadukan teknologi dan gaya hidup. Satu lagi produk Asus …

Harga Asus Zenfone 4 Max Pro, Spesifikasi, Kelebihan dan Kekurangannya
Asus terus berusaha mempertahankan keunggulannya dalam memadukan teknologi dan gaya hidup sebagai esensi dari Zenfone …

Harga dan Spesifikasi Asus Zenfone Max M1 Terbaru
Seperti biasa Asus selalu berusaha memenuhi kenyamanan pengguna HP dengan terus mempertahankan keunggulannya dalam memadukan …
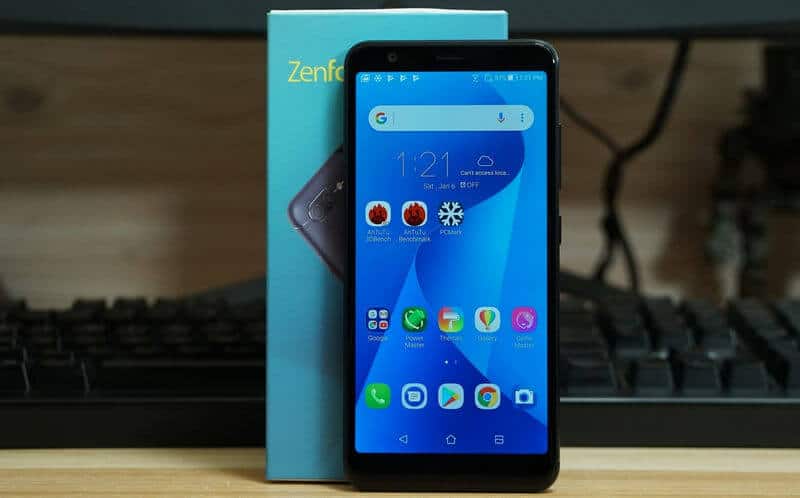
Spesifikasi dan Harga Asus Zenfone Max Plus (M1) Terbaru
Setelah meluncurkan Zenfone Max (M1) dengan keunggulan pada daya baterai, Asus kembali memperbaharui HP tersebut. …
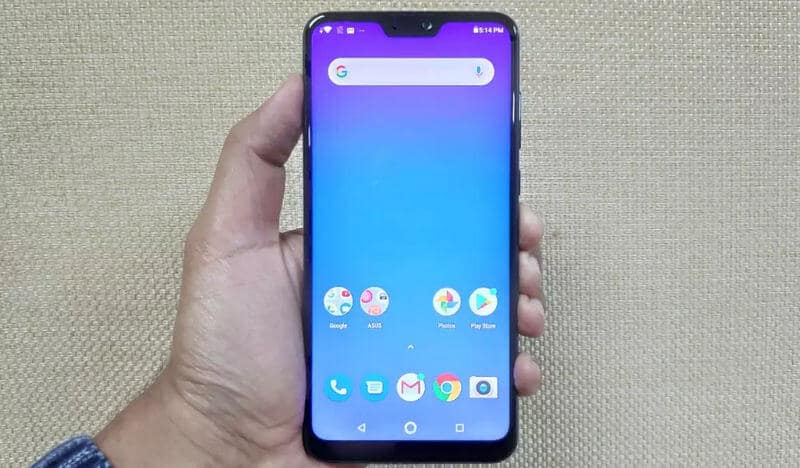
Harga Asus Zenfone Max Pro, Spesifikasi, Kelebihan dan Kekurangannya
Satu lagi produk HP Asus yang patut menjadi pilihan bagi pengguna HP. Produk bernama Asus …

Harga Asus Zenfone Live (L1), Spesifikasi, Kelebihan dan Kekurangan
Asus benar-benar mempertahankan esensi dari Zenfone. Satu kesatuan yang memadukan antara teknologi dan gaya hidup. …
